C3.4 - Ordenes de consulta.

Dentro del amplio repertorio de órdenes que se incluyen dentro del AutoCAD, hay varias que se utilizan como consultas de diverso tipo sobre la información que se va incluyendo en el archivo de dibujo. Normalmente se agrupan por su propia función en una barra de menú, panel o agrupación específica.

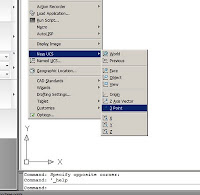
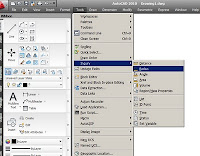
Dentro del los menús de persiana en la columna “Tools (Herramientas)”, se encuentra una entrada “Inquiry (Consulta)” en la que se agrupan: “Distance (Distancia)”, “Radius (Radio), “Angle (Angulo)”, “Area (Área)”, “Volume (Volumen)”, “Mass Properties (Propiedades de Masa)”. “List (Lista)”, “ID Position (Posición). “Time (Tiempo)”, “Status (Estado)”, “Set Variable (Variables)”.

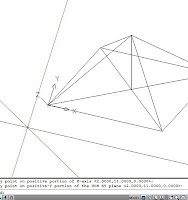
Distance (Dist)

Se trata de una orden que sirve para medir distancias dentro del dibujo. Cuando se ejecuta la orden, el sistema lanza un primer mensaje solicitando que señalemos un primer punto, a continuación, solicita un segundo punto y presenta la información del resultado que recopila la distancia y el ángulo entre los puntos señalados, y el valor de las componentes en ambos ejes.

La designación del segundo punto mantiene la visualización de un cursor elástico vinculado al primero que resulta muy útil, y la información se presenta en la línea de órdenes, o en la pantalla de texto (ocupa varias líneas), o bien si tenemos activada la “entrada dinámica” se presenta en la pantalla de forma mucho más clara.

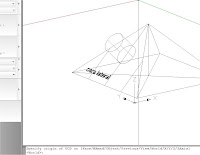
La orden también dispone de la opción “múltiples puntos”, en la que se puede entrar escribiendo en la línea de ordenes, antes de designar el punto, la “letra mayúscula” y un espacio a continuación. En este caso va presentando los datos parciales de una sucesión de segmentos, y el valor acumulado. También permite medir la longitud sobre el desarrollo curvo de “arcos” eligiendo la opción correspondiente.

Radius (Radio)

En este caso es una opción dentro de una orden “Measuregeom (Medirgeom)”. Se accede a ella a través de distintas opciones personalizadas según cada tipo de menú. Cuando se ejecuta esta opción, el sistema mediante un mensaje solicita la designación de un circulo, o un arco, y a continuación presenta como resultado los valores del radio y el diámetro en unidades de dibujo.

Angle

Se trata de otra de las opciones de la misma orden. En este caso al entrar en la opción, se desarrolla otro submenú con cuatro opciones, Arco, Círculo, Línea ó Designar vértice, que permite designaciones directas de arcos o bien combinaciones de círculos, posiciones y/o líneas, hasta definir un ángulo, dado como resultado un mensaje con su valor en las unidades configuradas.

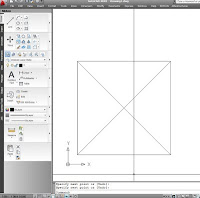
Area

En este caso al igual que con distancia, existe una orden independiente y directa, aunque también funciona integrada dentro del conjunto anterior.

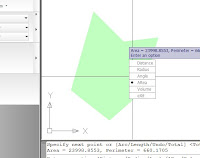Las opciones disponibles permiten designar distintos tipos de objeto de forma directa, o bien señalar gráficamente una sucesión de puntos. Finalmente con un mensaje sobre la línea de órdenes o por la entrada dinámica, se presentan los valores de área y perímetro en unidades de dibujo. Los objetos reconocibles en esta orden son los círculos, polígonos y polilíneas abiertas o cerradas, regiones y sólidos.

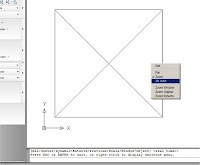
Dentro de las opciones particulares se encuentran además modos “adictivo” y “sustractivo” de forma que se permite designar una sucesión de objetos, presentando sucesivamente los valores acumulados, como suma o resta, hassta que cortamos la secuencia con una respuesta nula o “intro”.

En el caso que el objeto designado sea una región se debe tener en cuenta que pueden tener huecos, en cuyo caso se descuentan automáticamente, que se identifican con un sombreado temporal, y en el caso de objetos “sólidos” los valores dados corresponden a la suma de superficie de todas sus caras.

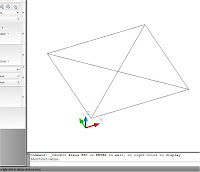
Volume

Es otra opción integrada en “Measuregeom”, y funciona prácticamente igual que la de Área, con la diferencia que cuando designamos entidades planas, finalmente se solicita una “altura” que también puede ser un valor numérico designado por teclado.

Mass Properties

En este caso es una opción que solo funciona sobre objetos de tipo “región” o sólidos, aunque en este caso suministra un conjunto de información mas ámplia y sofisticada, como es Masa, Volumen, Centro de Gravedad, y momentos de inercia en los tres ejes del espacio.

La información en este caso se presenta en la ventana de texto, y el sistema nos da la opcion para escribirla en una archivo de texto plano, facilitando el nombre oportuno.

List

Esta es otra orden que funciona con la designación de cualquier entidad del dibujo y a continuación suministra en la ventana de texto, toda su información asociada en forma de datos, la cual varia dependiendo de cada tipo de entidad. Suele incluir datos como nombre de la capa, color, tipo de línea, coordenadas, longitud etc.

De todas formas con la orden “Properties (Propiedades)” se consigue algo parecido aunque presentado en un cuadro de paleta, en lugar de la ventana de texto

ID Position

Esta es otra orden que una vez ejecutada, a traves del mensaje del sistema solicita que se designe un “punto” y a continuación presenta el valor de sus coordenadas en el sistema actual.

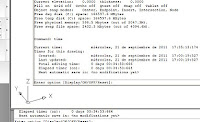
Time

Esta orden opera presentando en la ventana de texto, el momento actual con fecha y hora, y tambien el momento de creación del archivo de dibujo, el de la última actualizacion, y el tiempo transcurrido. Incluso con las opciones oportuno, permite definir un contador de tiempo parcial y reseteable vinculado al archivo de dibujo. 

Status

Esta es otra orden que presenta informacion en la ventana de texto correpondiente al archive de dibujo en curso, como el número de entidades que contiene, lo valores de capa, color, tipo de linea actuales, etc.

Set Variable

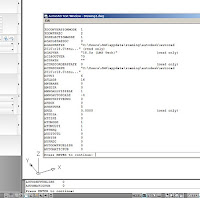En este caso se puede escribir como “Set” en la línea de ordenes, y el sistema responderá con un mensaje, solicitando el nombre de una de las variables internas del sistema, en cuyo caso mostrará el contenido de su valora, facilitando en su caso la posible modificación del mismo.

No obstante en lugar de dar un nombre concreto, admite una la “?” como opción, y luego la escritura de plantillas, como por ejemplo “dim*” en cuyo caso se presenta en la ventana de texto, la lista de todas las variables que se ajustan, a esa plantilla.

C3.3 - Consideraciones sobre el trabajo en 3D y/o 2D

Ya se ha mencionado de forma somera en el tema anterior, alguna diferencia entre el trabajo técnico habitual, en dos y tres dimensiones. No obstante parece oportuno comentar algo más la diferencia entre ambos planteamientos a la hora de abordar el trabajo técnico con las herramientas informáticas que ponen a nuestro alcance los ordenadores actuales.

Aquellos que hemos desarrollado una cierta edad en el ejercicio profesional, desde unos orígenes basados en el trabajo manual dentro de los estudios, y hemos asistido en primera fila al drástico cambio que ha supuesto la incorporación de las herramientas informáticas, hemos asistido paulatinamente a una curiosa e interesante confrontación, entre las “promesas” y “tendencias” que nos podían alcanzar en poco tiempo, y la vertiginosa evolución “real” que íbamos observando.

Evidentemente muchos de los “vaticinios” de evolución inmediata, han ido fallando inexorablemente, y sin embargo otros aspectos que casi nadie vaticinaba, acaban imponiendo cambios aplastantes. En este sentido cabe mencionar  a modo de ejemplo el uso de la telefonía móvil, cuando esta se consideraba una herramienta de gran utilidad en ámbitos profesionales, pero que sin embargo fue esa ansiedad y preocupación tan femeninas hacia los hijos adolescentes, la que introduce el artilugio en sus bolsillos sin la menor contemplación, y acarrea un resultado espectacular sobre los SMSs, que jamás habían  “vaticinado” las grandes compañías de telefonía móvil.

 

En los primeros momentos que aparecen sistemas informáticos relacionados con el ámbito profesional de la arquitectura y la edificación, estos se dedican a tareas auxiliares en consonancia con la gran capacidad para el calculo numérico “calculo de estructuras” y facilidad en el manejo de bases de datos, “elaboración de presupuestos y mediciones”. Esa etapa se desarrolla a lo largo de la década de los 80s, en la primera mitad de forma testimonial y en la segunda con una relativa pujanza, que al final de la década acaba arrinconando la  vieja “maquina de escribir”.

Al comenzar la década de los 90s, aparecen ya los primeros “iniciados” que conocen el programa “AutoCAD”, y también ordenadores más potentes, monitores y tarjetas gráficas especiales, y por supuesto el correspondiente “plotter” (..de plumillas), que se convierte casi de inmediato en el verdadero “artilugio” con capacidad para convencer a cualquier “escéptico”, y de paso admirar y aterrorizar a delineantes  recién salidos de la formación profesional, que habían proyectado sus expectativas, en la destreza con el dibujo manual.

Ya en aquellos momentos se “oían” algunos debates o discusiones de “barra de bar”, entre arquitectos iniciados, sobre la “revolución” que se avecinaba, dando casi por sentado el hecho de que en un futuro más o menos próximo, el dibujo de un proyecto arquitectónico, se abordaría  construyendo el modelo completo en “tres dimensiones”, con la promesa de una visualización fácil e inmediata desde cualquier punto de vista, y de tal forma que los planos tradiciones (plantas, alzados y secciones) serían solo el resultado de definir sus posiciones en el modelo, dejando al sistema informático la tediosa tarea  de gestionar la “elaboración automática” de aquellos planos que fuesen necesarios. (.. por cierto, ¿alguien recuerda la oficina sin papeles? )

Evidentemente aquel paradigma incluso en origen, pecaba de ilusorio y optimista, y aquellos vaticinios han sido archivados en el “anecdotario”. No obstante se sigue observando ocasionalmente un brillo especial en la mirada de algunos jóvenes, que se acercan a este mundo a través de un aprendizaje ilusionado y ansioso, y si se escucha con atención, se oye galopar su imaginación con el afán de dominar la navegación por ese nuevo mundo virtual de geometría espacial y modelos informáticos.

Obviamente la capacidad de seducción que genera la posibilidad de examinar desde cualquier punto de vista, o hacer un recorrido a través de un modelo virtual del edificio que hemos imaginado, incluso con el aspecto de sus materiales o una iluminación sofisticada, resulta especialmente cautivadora, y ha supuesto un avance indiscutible que poca gente podía imaginar hace poco más de veinte años, cuando la única aproximación a este mundo, era una laboriosa construcción de maquetas.

Esa gran capacidad de seducción también tiene el riesgo de desbocar la imaginación con un optimismo excesivo, que se puede manifestar desde un manierismo exacerbado en las formas que se proyectan, hasta el oportunismo mediocre y profano que trata de reemplazar un trabajo serio de “arquitectura” mediante sistemas informáticos y presentaciones deslumbrantes. Una vez glosados los elogios hacia las “tres dimensiones” y a ese nuevo mundo de posibilidades deslumbrantes, cabe hacer algunas “advertencias” si queremos dejar las cosas en su sitio.

En primer lugar hay que decir que el trabajo en “tres dimensiones” es intrínsecamente más complejo y por tanto laborioso y costoso en dedicación, tiempo y recursos. Por otra parte la utilidad que tiene los “planos” que se incorporan en ese documento que llamamos “proyecto técnico”, es la de servir de base tanto para la ejecución de las obras de construcción, como para dejar constancia previa, documentada y verificable, de aquello que se trata de construir, justificando los requisitos que condicionan las autorizaciones competentes.

Obviamente los dibujo en “dos” dimensiones (plantas, alzados y secciones) resultan más fáciles de elaboración, pero también tienen otra gran utilidad,  y es el hecho de que las dimensiones de los objetos que representan se encuentran en “verdadera magnitud”, es decir que se pueden medir, verificar o comprobar distancias, sobre el dibujo de forma directa sin otra consideración que la “escala” del dibujo.

Cualquier estudiante de geometría, sabe que para representar objetos espaciales en una superficie plana es necesario algún tipo de proyección, y aunque en todo caso exista una relación que permite determinar distancias y posiciones con rigor matemático, en el caso de las proyecciones cónicas las “distancias” se distorsionan en función de su posición respecto al eje de proyección, y en el caso de las proyecciones paralelas, aunque la distorsión se mantenga constante a lo largo de cada dirección,  también varia en función de estas, por lo que cualquier comprobación de posiciones o distancias en un “plano” dibujado en perspectiva, se convierte en una tarea con una “complejidad matemática”, que lo deja fuera de ese tipo de uso. 

Evidentemente y como conclusión a estas consideraciones, creo que cabe “vaticinar” sin temor a equivocaciones sobre la evolución del futuro, que el uso de los “planos” para la construcción de obras y otro tipo de objetos, se seguirá realizando en dos dimensiones (o sistema diédrico de proyección) durante muchas generaciones sucesivas.

Llegados a este punto y aunque solo sea por redundancia, cabe recordar aquellas “láminas de dibujo”, que se estudiaban en las escuelas de arquitectura del siglo XIX, sobre “estereotomía de la piedra”, en las que se mostraban métodos geométricos, para el trazado de las formas mediante el “abatimiento” de planos, desarrollos en verdadera magnitud, y métodos parecidos, que luego permitían construir las “plantillas” y “baiveles” que guiaban a los canteros en la fabricación de “sillares” y “dovelas” de piedra, que cuando eran “levantadas” y “colocadas” con esfuerzo considerable, tenían que encajar entre si con la exactitud suficiente para asegurar la estabilidad del conjunto.

C3.2 - Sistemas de coordenadas personales y globales

Hasta ahora hemos considerado puntos y coordenadas, en dos o tres dimensiones, pero siempre respecto a un “origen” único y común a todas las referencias.

Implícitamente dentro de las tres dimensiones espaciales que el programa maneja ( X,Y,Z ) existe una preponderancia de un “plano principal de trabajo” que normalmente es el “XY”, ya que la mayoría de entidades, salvo los puntos y segmentos individuales de línea, tienen una configuración propia, que necesariamente tiene que estar contenida en “un plano” cualquiera. Por ejemplo, cuando definimos un rotulo de texto, este se sitúa sobre un punto que puede estar en cualquier posición del espacio, pero al configurar el “rótulo” las letras quedan orientadas “necesariamente” dentro de un plano paralelo al “XY” que pasa por el punto que acabamos de señalar.

El proceso normal de construcción y definición de la geometría, hace uso habitual de esa característica, de forma que los “datos” que se van solicitando en cada momento se simplifican, restringiendo la ubicación a ese plano principal, o bien a otro paralelo. Esto es así en parte porque la interfaz de pantalla es un espacio de solo dos dimensiones, y la designación gráfica de posiciones en 3D necesariamente tiene que implementar algún sistema que resuelva ese conflicto.

La forma de solventar el problema depende obviamente de la “filosofía” de cada sistema gráfico, y como ejemplo cabe mencionar el caso de SketchUp, donde se hace un manejo de las tres dimensiones bastante sutil y ergonómicamente elaborado, aunque también requiere una cierta información previa sobre las características y posibilidades menos frecuentes, además de un pequeño adiestramiento para lograr un uso eficaz.

En el caso de AutoCAD la opción adoptada tiene presumiblemente mucho que ver con un entorno del trabajo profesional, ya que en su mayoría los planos técnicos de uso habitual, se realizan normalmente en dos dimensiones, asegurando entre otras cosas, que la geometría de los objetos se muestra en “verdadera magnitud” y por tanto cualquier proceso para definir y/o comprobar sus dimensiones, resulta más inmediato, simple y con menor riesgo de errores. No obstante el uso de geometrías y modelos completos en 3D, con un control sobre el aspecto de los materiales y la iluminación, también es una herramienta imprescindible para mostrar el aspecto final, y poder transmitir a terceros, las ideas que han servido para concebir un determinado proyecto.

Sistema de Coordenadas Personales:

En AutoCAD, la forma de poder orientar los objetos o entidades en cualquier dirección del espacio, se realiza con el uso de los sistemas de coordenadas particulares o personales, que el usuario puede definir a su propia conveniencia, de forma que puede “orientar” el plano de construcción “XY”, en cualquier dirección del espacio y a partir de ahí, definir y colocar cualquier objeto o entidad en dicha orientación, aunque el objeto en sí este contenido en su propio plano.

Esta característica lleva a considerar el sistema de coordenadas inicial, como “Sistema Global de Coordenadas” o coordenadas absolutas, de forma que siempre se puede volver a él desde otro cualquiera, y sobre él se definen los demás sistemas de coordenadas personales, o relativas.

El uso y la definición de los sistemas de coordenadas personales se realiza con la orden “UCS” directamente desde línea de ordenes o bien con “DDUCS”, a través del cuadro de dialogo correspondiente. También esta disponible en las distintas opciones de menú, con un repertorio amplio de alternativas inmediatas que facilitan algunas definiciones particulares del nuevo sistema. De todas formas el modo más completo o general para definir cualquier sistema de coordenadas, es la de “3 puntos”, de forma que al definir una secuencia de tres puntos en el espacio, se sitúa en el primero de ellos el nuevo origen de coordenadas, con el segundo punto se sitúa la parte positiva del eje X, y el tercero junto con los anteriores, define la parte positiva del nuevo plano XY.

Además de esta forma que resuelve el caso más general, existen otras opciones más simplificadas e inmediatas dentro del menú habitual, como las de “Cara”, “Objeto” y “Vista”, que alinean los nuevos ejes con el tipo de entidad designada, o bien “Origen” y “eje Z”,  que en el primer caso reubica solo el nuevo origen manteniendo la orientación de ejes, y en el segundo ajusta el eje Z sobre un par de puntos. También hay opciones para girar ángulos determinados respecto a cada uno de los tres ejes. Otras dos opciones y quizá las de uso más común, son la de asignar un “nombre” al sistema de coordenadas personal, de forma que se pueda retornar a él seleccionando el nombre en una lista, y la de volver al sistema Global o Universal que además es la opción por defecto.

                                                                                                               

Las opciones de la orden UCS, evidentemente se complementan con otras características para facilitar el movimiento del punto de vista, y a su vez la designación de los objetos, con el fin de poder trabajar cómodamente en 3D. Una de las ordenes tradicionales para este fin es “PTVIEW”, que permite designar cualquier punto del espacio, para representar la geometría mediante una proyección paralela, según la dirección que une el punto designado con el origen de coordenadas. Esa orden también dispone un grafico para la designación dinámica pero resulta algo complejo de uso ya que representa la superficie de una esfera con dos circunferencias concéntricas, de modo que la interior corresponde al hemisferio “norte” y el espacio entre las dos circunferencias al hemisferio “sur” o en otras palabras a una vista desde “abajo”.

Esta orden actualmente se encuentra obsoleta y en desuso. En la actualidad hay otros modos más intuitivos y directos para “mover” el punto de vista, como la orden “ORBIT”, que se encuentra también disponible en el menú contextual vinculado  al “ZOOM DINAMICO”, y que a su vez dispone de las variantes libre y restringida, según se mueva el punto de vista solo alrededor del eje ortogonal a la pantalla, o bien en cualquier dirección del espacio mediante una mira auxiliar.

Cuando se modifica el punto de vista, resulta útil la información que facilita el icono de orientación, el cual puede cambiar de aspecto con los estilos de visualización, y siempre representa la orientación de los ejes de coordenadas. Dispone de un “cuadrado” que se sitúa en el vértice si nos encontramos en el sistema “global”, el cual desaparece cuando pasamos a otro sistema personal o particular.  Cuando la proyección del espacio no es plana, también los ejes que constituyen el cursor se visualizan con un código de color “rojo” para el elje X, “verde” para el Y y “azul” para el Z.

Otra orden que resulta útil cuando queremos volver a la proyección ortogonal del plano XY, en la orden “PLAN” o “planta”, que con una pulsación de confirmación, nos devuelve a la representación ortogonal del plano XY referida al sistema de coordenadas en curso.

C3.1 - Uso de coordenadas. Definición de puntos y distancias.

Como ya se ha dicho en capítulos anteriores, el trabajo cotidiano dentro del programa, se realiza sobre un espacio virtual que inicialmente se encuentra en “blanco” pero en todo caso mantiene un “sistema de coordenadas” cartesiano. Este espacio virtual es prácticamente “ilimitado”, siendo su única restricción, el rango o tipo de números que maneja el sistema operativo para definir las “coordenadas” de cada posición o elemento dentro de ese espacio virtual. 

Es conveniente distinguir con claridad la diferencia entre ese espacio ilimitado, y el área que se visualiza en pantalla cuando se comienza un nuevo dibujo, la cual depende exclusivamente de la definición previa que se haya hecho en el dibujo prototipo o plantilla sobre la que hayamos iniciado el trabajo, o configurado por defecto. (“acad.dwg”, “acad.dwt”, “acadiso.dwt”, .. etc.). 

Cuando se inicia cada dibujo, adoptamos implícitamente un “origen” de coordenadas, y comenzamos a situar elementos geométricos que nos permiten construir el modelo respecto a él, y vamos midiendo distancias o situando posiciones de acuerdo con los principios habituales de la geometría. Normalmente se adopta el eje X como horizontal, con su parte positiva hacia la derecha, el eje Y como vertical con su parte positiva hacia la zona superior de la pantalla,  situando el origen de coordenadas en la esquina inferior izquierda, y el eje Z perpendicular a la pantalla con su parte positiva hacia fuera, de acuerdo con el sentido “dextrógiro” X>Y>Z. 

Cuando trabajamos habitualmente, lo  normal es que dibujemos un edificio o cualquier otro objeto de uso cotidiano. Los valores numéricos de sus dimensiones dependen del significado que asignamos a cada unidad de longitud que normalmente son “metros”, pero también podemos utilizar “kilómetros” o “milímetros”. Esta decisión junto con el tamaño del objeto que se dibuja, determinan el área que normalmente visualizamos en la pantalla, dependiendo del factor de zoom que aplicamos en cada momento. 

La situación del “origen de coordenadas” es poco relevante a la hora de construir un dibujo, ya que es la “distancia” relativa entre las posiciones de sus elementos, la que define el tamaño del objeto y finalmente configura la geometría del mismo. El programa dispone  de un “icono” que representa la orientación del sistema de coordenadas en cada momento, y puede estar ubicado en la esquina inferior izquierda de la pantalla, o bien forzar su ubicación identificando la posición del origen de coordenadas.

Hay que advertir que en algún caso pueden darse circunstancias que generan desconcierto o confusión, como por ejemplo cuando al hacer un “zoom” sobre la extensión de un dibujo, nos encontramos prácticamente con una pantalla en blanco, aunque si nos fijamos con algo de detenimiento observamos cierto movimiento en un punto minúsculo y extraño situado por algún borde de la pantalla.

Cuando utilizamos dibujos procedente del ámbito de la cartografía, es común que estén “georreferenciados”, con arreglo a especificaciones como el sistema UTM, que divide la superficie del planeta en “husos” numerados hacia este y oeste, situando cada origen de coordenadas en la intersección entre el “ecuador” y el meridiano izquierdo que lo define. Eso supone que en esos archivos de dibujo, las coordenadas suelen ser números relativamente grandes, (valores de 300.000 a 4.700.000 expresadas en metros, para latitudes habituales en España). 

Si hacemos un “zoom” sobre la “extensión” del dibujo normalmente se visualiza la hoja del mapa o plano con independencia del origen de coordenadas, no obstante si en algún caso hemos “insertado” mediante una referencia externa “XREF” un archivo georreferenciado y dibujamos algún objeto, si posteriormente al volver a abrirlo en otra ocasión hemos perdido la trayectoria de la referencia, cuándo hagamos “zoom-extensión” se visualizará el contorno de nuestro objeto en su posición, pero también un “rotulo” de la referencia perdida situado precisamente en el “origen de coordenadas” y por tanto a la altura del “ecuador”. Naturalmente la visualización de todo el espacio comprendido entre el ecuador y nuestro objeto hace que circunstancialmente se pierda la percepción de los objetos dibujados.

Este problema aún puede acentuarse, si en la configuración de la orden “UNITS” o “unidades”, uno de los archivos se interpreta como “milímetros” o “pulgadas” y el otro en “metros”, ya que el dibujo insertado puede multiplicar sus dimensiones propias, por la relación entre las unidades predeterminadas en ambos archivos. 

Puntos y Distancias

La definición de puntos y/o posiciones gráficas, puede hacerse indistintamente marcando directamente mediante el ratón, sobre la posición que ocupa el cursor en cada momento, o bien escribiendo a través del teclado los valores numéricos de las coordenadas que definen la posición deseada. En este último caso, es preciso conocer y respetar la sintaxis correspondiente, pero en todo momento cuando una “orden” del programa espera la designación de un “punto” es perfectamente posible utilizar cualquiera de las dos formas, o sus variantes.

La sintaxis normal para escribir “puntos” en la “línea de órdenes”, es la de una cadena de dos ó tres números reales separados por comas: <“x.x,y.y,z.z”> sin espacios intermedios. La secuencia de números es interpretada en el momento que se pulsa la tecla “intro” o bien la barra espaciadora, razón por la cual resulta incompatible la incorporación de “espacios” dentro de la secuencia.

Al escribir los números es posible “omitir” tanto la parte entera como la decimal,  pero el valor numérico siempre se interpreta como “real”. Si en la secuencia numérica solo se escriben dos números, estos se interpretan como coordenadas X e Y, y como valor para la coordenada Z, se adopta “cero”, o bien el valor almacenado en la constante “ELEV”. 

El valor de las coordenadas numéricas que se definen por teclado, se interpreta como una posición absoluta respecto al origen de coordenadas, no obstante es posible definir posiciones “relativas” respecto al último punto que se haya designado, por cualquiera de las formas posibles, anteponiendo en la cadena el símbolo “arroba”, es decir “@x.x,y.y,z.z”. También es posible “alterar” esa notación de coordenadas para usar como referencia un sistema de coorddenadas “cilindricas” o “polares” solo con cambiar el separador, es decir la “,” (coma) por el signo “<” (menor que). 

Cuando escribimos “M.M<a.a” El valor real “M.M” se interpreta como una “distancia” al origen de coordenadas” y el valor “a.a” se interpreta como el valor del “angulo” sobre el que se mide esa distancia, en el plano horizontal. El origen de ángulos suele coincidir con el eje X pero se puede configurar mediante la orden “UNITS”, igual que el tipo de unidades angulares: (grados sexagesimales, centesimales, radianes etc.). Si la secuencia es de “dos” números el valor de Z se adopta como en el caso anterior, pero también es posible escribir “tres” números “M.M<a.a<b.b” en cuyo caso el valor de “b.b” se interpreta como el ángulo en el plano vertical que pasa por el punto (coordenadas esféricas).

La definición de distancias requier obviamente la designación de al menos dos puntos sucesivamente y se efectúa normalmente de una forma dinámica bastante intuitiva, ya que en la pantalla gráfica, se vincula una línea el elástica al primer punto designado, que se muestra hasta que queda señalado el segundo punto y definida la distancia correspondiente.

Para la definición de distancias fijas y precisas, el programa dispone de ciertos repertorios auxiliares como las “refent” o los “filtros” que se comentarán más adelante. No obstante un recurso bastante útil e inmediato, es el uso de “coordenadas relativas” que se acaba de comentar, ya que si después de haber señalado un primer punto, escribimos por teclado “@5.25,0”, estamos señalando otro “punto” que se encuentra exactamente a 5.25 unidades de distancia horizontal respecto al primero.

También es posible escribir en la línea de órdenes un solo número real, cuando el programa espera la entrada de una distancia o un segundo punto, de forma que el valor numérico aislado se interpreta como una “distancia” en unidades de dibujo, desde el punto señalado anteriormente y sobre la dirección apuntada por el cursor en ese momento.